О методике рассказывает руководитель центра компетенций по экономико-математическим методам консалтинговой компании «А ДАН ДЗО» Л.В.АНТОНЯН, кандидат физико-математических наук.
Автор: Л.В.АНТОНЯН, руководитель центра компетенций по экономико-математическим методам консалтинговой компании «А ДАН ДЗО», кандидат физико-математических наук.
Оптимизация управления запасами материально-технических ресурсов (МТР) имеет своей целью минимизацию расходов на содержание запасов при обеспечении требуемого уровня обслуживания (удовлетворения потребностей) потребителей.
Поскольку нехватка производственных запасов чревата нарушением ритмичности производства, снижением производительности труда, перерасходом МТР из-за вынужденных нерациональных замен и, как следствие, повышением себестоимости выпускаемой продукции [1], а наличие неиспользуемых запасов увеличивает затраты на их содержание (прежде всего, отвлекает из оборота денежные средства), то поддержание оптимального уровня запасов и рациональной динамики их пополнения является весьма актуальной задачей.
На Западе, где методы оптимизации управления производственными и сбытовыми запасами известны достаточно давно, их применение позволяло некоторым компаниям снизить уровень запасов наполовину при одновременном улучшении обслуживания потребителей.
К сожалению, в отечественной практике зарубежные разработки в области управления запасами до недавних пор практически не применялись. Это связано с сильной зависимостью моделей управления запасами от основных хозяйственных механизмов, принципов ценообразования, налогообложения и т.д.
В последнее время интерес, проявляемый российскими предприятиями к современным методам управления запасами, стремительно растет. Значительными тиражами издается соответствующая литература. Но, к сожалению, на данном этапе уровень изложения материала в отечественных источниках зачастую невысок. Между тем, при внешней простоте некоторых моделей, их грамотное применение требует аккуратного учета целого ряда нюансов, которые в большинстве источников вообще не обсуждаются.
Наш подход к проблеме оптимизации управления запасами МТР базируется на следующих посылках:
Для классификации МТР предлагается выработать набор признаков, в зависимости от которых каждая номенклатурная единица будет отнесена к одной из групп (или категорий) МТР. В свою очередь, для каждой из этих групп будет предложена одна конкретная модель управления запасами.
Таким образом, сначала из всех возможных характеристик материально-технических ресурсов, циркулирующих в системе материально-технического снабжения предприятия, необходимо выделить наиболее важные из тех, которые могут так или иначе влиять на выбор стратегии управления запасами (понятно, что, например, цвет материала вряд ли попадет в число таких характеристик).
Наша методика предполагает использование следующего набора признаков.
1. Совокупная стоимость приобретения.
Имеется в виду совокупный - за весь период планирования - спрос (объем потребления) в денежном выражении. Если эти затраты достаточно велики, то соответственно велики и убытки от омертвления денежных средств, вложенных в запасы, и вообще - расходы на содержание запасов, так что в этом случае первостепенное значение имеет минимизация уровня запасов и соответственно, предпочтителен постоянный контроль уровня запасов и оптимизация объемов закупок. Если же вложения в запасы относительно невелики и затраты на хранение (признак 8) также относительно невелики, то на первый план выходят другие задачи: минимизация расходов на организацию поставок и на контроль запасов – и тогда, возможно, предпочтительнее периодический (например, раз в месяц или даже в год) контроль и пополнение запасов.
2. Совокупный спрос (потребность) в натуральном выражении.
Если объем потребления рассматриваемого ресурса достаточно невелик (и сопоставим с минимальной партией поставки), то, вероятно, наиболее предпочтительной стратегией будет обеспечение потребностей на весь период планирования (например, на год) одной поставкой, что позволит минимизировать расходы на организацию поставок и контроль запасов.
3. Характер динамики спроса (объемов потребления).
При постоянных или слабо меняющихся объемах спроса хорошо работает модель оптимальной партии заказа или периодический контроль запасов с их пополнением до фиксированного максимального уровня, выбор между которыми определяется другими признаками. При значительно, но плавно меняющемся спросе лучше применять динамические модели пополнения запасов. Если же спрос меняется скачкообразно или имеет «импульсный» характер (когда отдельные «выбросы» спроса сопровождаются длительными периодами его полного отсутствия), то единственной возможной стратегией будет, скорее всего, удовлетворение потребностей по мере их возникновения с последующим (или, напротив, упреждающим) пополнением запасов.
4. Критичность.
К критичным относятся те ресурсы, отсутствие которых может привести к значительному (или даже невосполнимому) ущербу, например, вследствие аварии, остановки производства, и к необходимости организации экстренных поставок. Типичный пример некритичных ресурсов - материалы и запасные части, применяемые при проведении планово-профилактических мероприятий (которые относительно безболезненно могут быть отложены).
В предлагаемой схеме классификации критичность непосредственно не влияет на выбор модели управления запасами, однако она определяет необходимость содержания страхового запаса: для критичных ресурсов он обычно необходим, а некритичных - не нужен. Таким образом, можно сказать, что для критичных и некритичных МТР мы рекомендуем применять различные модификации одних и тех же моделей (со страховым запасом и без такового соответственно).
5. Надежность поставок.
Важным параметром любой модели управления запасами является время доставки закупленной партии МТР от поставщика, поскольку оно непосредственно влияет на уровень запаса, при котором необходимо организовывать очередную поставку. Но важно также, насколько этот временной интервал может меняться (от поставки к поставке) под воздействием тех или иных случайных факторов (в частности, при собственных закупках существенное влияние здесь может иметь дефицитность искомого МТР на рынке). И если время поставок практически не меняется, то поставки считаются надежными, а если оно испытывает существенные колебания (как, к сожалению, часто случается в российских условиях), то - ненадежными (возможность отклонения фактического объема поставки от заказанного не рассматривается). В предлагаемой схеме классификации этот признак, как и предыдущий, на выбор модели непосредственно не влияет, но он влияет на величину страхового запаса.
6. Интервал между поставками (фиксированный или произвольный).
Условия поставок могут предусматривать либо фиксированный интервал между поставками (например, 1 месяц), либо произвольный (по требованию заказчика). Во втором случае возможно применение модели оптимальной партии заказа с постоянным контролем запасов и их пополнением при снижении складского запаса до уровня так называемой «точки заказа». В первом же случае осуществляется периодический контроль запасов и их пополнения в требуемых (вообще говоря, переменных) объемах.
7. Издержки постоянного контроля запасов (высокие или низкие).
Этот признак определяет возможность и целесообразность постоянного контроля уровня запасов. Постоянный контроль запасов предполагает доступность информации об уровне запасов в любой момент времени (или, по крайней мере, один раз в сутки). Ясно, что такой контроль может быть целесообразен только для МТР с достаточно большим спросом (уровнем потребления), хотя даже и в этом случае он может и не требоваться (например, при стабильном уровне потребления уровень складского запаса может быть предсказан и без обращения к фактическим данным). В то же время, если даже все прочие условия диктуют целесообразность именно постоянного контроля, такой контроль может оказаться либо слишком обременительным (т.е. дорогостоящим), либо вовсе невозможным (например, по чисто техническим причинам). В таком случае практическое применение модели оптимального заказа (в ее классическом толковании) становится невозможным, и следует обратиться к другим схемам.
8. Затраты на хранение (высокие или низкие).
Здесь имеются в виду затраты на содержание запасов за вычетом стоимости вложенного в них капитала (т.е. эксплуатационные расходы, заработная плата и т.д.), хотя реально выбор модели управления запасами зависит именно от суммарной величины расходов на содержание запасов (включая стоимость отвлеченных оборотных средств). Тем не менее, этот признак включен в схему классификации, поскольку возможна (и даже характерна!) ситуация, когда расходы на хранение запасов исчисляются как усредненная по множеству номенклатур фиксированная доля от их стоимости и расходы на хранение малоценных МТР оказываются ничтожно малыми, что может приводить к существенным искажениям реальной картины: ведь даже малоценные МТР (например, гигроскопичные) могут требовать определенных условий хранения, что, естественно, повышает расходы на их хранение. Это диктует целесообразность выделения в составе расходов на хранение запасов слагаемого, пропорционального их стоимости (в простейшем варианте это может быть стоимость капитала, вложенного в запасы) и отдельного рассмотрения тех статей (расходов на хранение), которые от цены данного МТР не зависят.
Таблица 1
|
№ |
Признак |
Значение |
Критерий |
|
Характеристики спроса |
|||
|
1 |
Совокупная стоимость приобретения |
2 |
Высокая: 5 - 10% номенклатур, суммарный спрос на которые в стоимостном выражении наиболее высок и в совокупности составляет до 65% общего спроса на МТР |
|
1 |
Средняя: около 20% по составу и порядка 30% по стоимостному спросу |
||
|
0 |
Низкая: 70-75% по составу и около 5% по стоимостному спросу |
||
|
2 |
Объем спроса (в натуральном выражении) |
1 |
Высокий или средний: минимум на 1-2 порядка превосходящий объем минимальной партии заказа |
|
0 |
Низкий: сопоставимый с минимальной партией поставки |
||
|
3 |
Характер динамики спроса |
2 |
Скачкообразно меняющийся во времени или дискретный (в последнем случае имеется в виду чередование «выбросов» высокого спроса и достаточно длительных интервалов его отсутствия) |
|
1 |
Существенно, но плавно меняющийся во времени |
||
|
0 |
Постоянный или слабо меняющийся во времени: коэффициент вариации суточного объема спроса (отношение среднеквадратического отклонения к среднему спросу) меньше 0,2 |
||
|
4 |
Критичность |
1 |
Высокая: отсутствие данного МТР может нанести существенный ущерб, например, в результате остановки производственного процесса и/или выхода из строя дорогостоящего оборудования |
|
0 |
Низкая: временный дефицит данного МТР не приводит к существенному ущербу; например, если данный МТР используется при проведении планово-профилактических мероприятий, которые могут быть безболезненно перенесены на более поздний срок |
||
|
Характеристики поставщика |
|||
|
5 |
Надежность поставок |
1 |
Низкая (если вследствие ненадежности поставщика или дефицитности данного МТР на рынке (при собственных закупках) время пополнения запаса может существенно варьироваться) |
|
0 |
Высокая |
||
|
6 |
Интервал между поставками (по условиям поставщика) |
1 |
Фиксированный |
|
0 |
Произвольный |
||
|
Характеристики условий контроля хранения запасов |
|||
|
7 |
Издержки постоянного контроля запасов |
2 |
Высокие: постоянный контроль запасов нецелесообразен или невозможен |
|
1 |
Средние: целесообразность постоянного контроля запасов зависит от значений других признаков |
||
|
0 |
Низкие. В многономенклатурном (порядка нескольких десятков тысяч позиций) складском хозяйстве снижение издержек (и даже сама возможность) постоянного мониторинга запасов обеспечивается внедрением автоматизированной системы управления складом или комплексной автоматизированной системы управления предприятием. |
||
|
8 |
Затраты на хранение |
1 |
Высокие |
|
0 |
Низкие |
||
Возможные значения каждого из признаков (0, 1, ...) и их интерпретации приведены в таблице 1. Для всех признаков соблюдается один и тот же принцип: МТР с более высокими значениями признака с соответствующей точки зрения более «проблемны» и должны рассматриваться в первую очередь. Именно поэтому, к примеру, по признаку 6 МТР с фиксированным интервалом между поставками получают 1 балл, а с произвольным интервалом - 0: ведь в первом случае приходится иметь дело с серьезным ограничением, тогда как во втором варианте свобода маневра - по крайней мере, с рассматриваемой точки зрения - сохраняется. Другой пример: для МТР с высокой стоимостью приобретения (для которых значение соответствующего признака равно 2) оптимизация управления запасами (причем в первую очередь - минимизация уровня запасов и, соответственно, оптимизация объемов поставок) может принести значительный эффект, тогда как для малоценных МТР (с оценкой 0) аналогичные усилия могут оказаться малопродуктивными. Но только в том случае, если и затраты на их хранение невелики! Тем не менее, некоторые из малоценных МТР с невысокой стоимостью хранения вполне могут оказаться «критичными» для производственного процесса (признак 4) и как таковые не должны выпасть из поля зрения. Правда, здесь, вероятно, в первую очередь потребуется обеспечить надлежащий уровень страхового запаса.
Вместо числовых значений (0,1....) признаков можно было бы использовать буквенные коды, как, например, это принято в АВС-анализе. Однако предлагаемая схема предпочтительнее в том отношении, что она позволяет легко комбинировать предложенные признаки, вводя в рассмотрение те или иные интегральные показатели в виде линейных комбинаций (например, сумм) значений данных признаков (а, возможно, и их произведений) и ранжировать МТР по значениям таких интегральных показателей. Например, можно скомбинировать (сложить или умножить) признаки 3, 4 и 5 и использовать полученный интегральный показатель в качестве мерила необходимости использования страхового запаса.
Рассматривается простейшая однопродуктовая модель управления запасом некоторого материально-технического ресурса, включающая:
На практике поставщиков, как и потребителей, может быть несколько, но в рассматриваемых моделях они объединяются в одного совокупного поставщика (соответственно - потребителя).
Если речь идет о складе сырья и материалов на производственном предприятии, то в роли поставщиков могут выступать внешние производители или дистрибьюторы сырья и материалов, а в роли потребителя – собственное производство. Если же имеется в виду склад готовой продукции, то производство выступает уже в роли поставщика, а в роли потребителей – внешние покупатели производимой продукции. Возможны и варианты, когда никакого производства нет вообще – например, если рассматриваемое предприятие само является дистрибьюторской компанией или магазином розничной торговли.
Параметры модели управления запасами, которыми можно управлять (объемы поставок, интервалы между поставками и т.д.) подбираются таким образом, чтобы минимизировать совокупные затраты на пополнение и хранение запасов в течение всего заданного периода планирования (Тпл).
Единицей измерения времени может быть день, неделя, месяц и т.д.
Предполагается, что поставки осуществляются отдельными (дискретными) партиями, каждая из которых характеризуется объемом и временем поставки.
Объем партии (Q) может быть - в зависимости от условий поставки и принятой стратегии управления запасами - либо фиксированным, либо произвольным. В первом случае требуемый уровень запасов поддерживается путем регулирования интервала между поставками, а во втором варьироваться могут и объемы поставок.
Условия поставок могут также ограничивать минимальный (Qмин) и максимальный (Qмакс) объемы партии. Кроме того, может задаваться ограничение по кратности объема поставки некоторой величине Qтр (вагону, цистерне, контейнеру и т.д.) - минимальной транзитной партии. Например, если минимальная партия поставки составляет 100 тонн, а минимальная транзитная партия - 1 вагон (60 тонн), то возможные объемы поставок составят: 120 тонн (2 вагона), 180 тонн (3 вагона) и т.д.
Время поставки определяется условиями поставок и является, вообще говоря, случайной величиной (т.е. может варьироваться под влиянием различных случайных факторов). В действительности для оптимизации управления запасами важен промежуток времени от момента принятия решения на пополнение запасов (включая время на обработку соответствующей информации) до момента завершения процесса поставки (когда поставленные запасы распределены по местам хранения и готовы для отпуска потребителям). И в дальнейшем именно этот промежуток времени - время подготовки и исполнения заказа - будет фигурировать в качестве одного из параметров модели и именно он будет для краткости называться временем поставки.
Время поставки (как случайная величина) имеет стандартные числовые характеристики: среднее значение (математическое ожидание) L и среднеквадратическое отклонение σL. Величина σL определяет, насколько (в среднем) время поставки может отклоняться от своего среднего значения и, таким образом, может рассматриваться как характеристика надежности поставщика. В частности, если время поставки не меняется и равно, к примеру, 5-ти дням, то L = 5, σL = 0.
Спрос на хранимый материально-технический ресурс может быть стационарным (постоянным) или нестационарным (перемененным), детерминированным (известным) или случайным. Строго говоря, спрос всегда является случайной величиной (хотя обычно и может быть предсказан с той или иной степенью точности) и поэтому имеет смысл говорить о его числовых характеристиках: среднем значении (d) и среднеквадратическом отклонении (σd) объема спроса за единицу времени. Также имеет смысл говорить о величине (D) совокупного спроса за весь период планирования (Тпл). Очевидно, D = d×Тпл. Кроме того, при стационарном спросе σd = 0.
Динамика объемов складских запасов складывается как результат двух параллельных процессов: расходования запасов по мере удовлетворения текущего спроса и их пополнения посредством регулярных закупок (поставок). Влияние процессов порчи и устаревания на динамику запасов в рассматриваемых моделях не учитывается.
Предполагается, что процесс снабжения управляется следующим образом: каждая очередная поставка инициируется тогда, когда выполняется определенное условие (зависящее от принятой стратегии управления запасами), например:
Промежуток времени Т между двумя последовательными поставками будет в дальнейшем называться циклом поставок. При периодическом контроле запасов цикл поставок является постоянной величиной. В общем случае под циклом поставок будет подразумеваться среднее значение интервала между поставками.
Следует отметить, что при применении системы управления запасами с «точкой заказа» (s) текущий уровень запасов вполне может опускаться ниже этого порогового значения. Такая ситуация может возникнуть по крайней мере в двух случаях: а) при периодическом контроле запасов (когда проверка уровня запасов производится через фиксированный промежуток времени Т); б) при дискретном спросе (когда до отгрузки очередной партии рассматриваемого МТР потребителю уровень запаса может быть выше, а после отгрузки - существенно ниже «точки заказа»).
Применяемая стратегия управления запасами может предусматривать либо пополнение запасов равными (по объему и оптимальными в том или ином смысле) партиями, либо их наращивание до определенного максимального уровня (S). Возможны и более сложные стратегии, которые в дальнейшем будут обсуждаться отдельно.
Очевидно, что в условиях неопределенности (когда динамика спроса, сроки поставки и, возможно, другие параметры системы снабжения подвержены влиянию случайных факторов) возможны ситуации, когда текущий спрос на поставляемые МТР не может быть удовлетворен вследствие отсутствия требуемого их количества на складе. Тогда возникает так называемый «отложенный спрос» на поставляемые МТР (вариант потери спроса при невозможности его удовлетворения рассматриваться здесь не будет). Допустимость подобных ситуаций зависит от степени критичности рассматриваемого МТР для потребителей: если его дефицит приводит к значительным материальным потерям (например, вследствие аварий или остановок производства), то ситуация дефицита недопустима. Или, по крайней мере, необходимо свести вероятность ее возникновения к минимуму. Для этого в модель управления запасами вводится специальный параметр - уровень (или надежность) обслуживания (р), который определяется как вероятность того, что в течение одного цикла поставок весь текущий спрос будет полностью удовлетворен.
Для достижения требуемого уровня обслуживания в составе складского запаса МТР выделяют специальную составляющую - страховой запас (qстр), объем которого в большинстве моделей принимается постоянным. Соответственно весь складской запас (qскл) распадается на две части: текущую (qстр) и страховую составляющие [2]:
qскл = qтек + qстр .
Текущий запас (уровень которого зависит, вообще говоря, от времени) предназначен для удовлетворения ожидаемого спроса, а страховой - для покрытия его случайных колебаний.
Если пополнение запасов производится регулярными поставками, то в идеальном варианте к моменту каждого очередного пополнения складской запас снижается до уровня страхового запаса. Если же часть страхового запаса расходуется на покрытие незапланированного увеличения спроса, то последующими поставками он восполняется до установленного уровня.
Как показывает практика, страховой запас в большинстве случаев составляет 30-50% от среднего уровня текущего запаса.
В следующих случаях страховой запас обычно не предусматривается:
Величина суммарного складского запаса qскл включает только те запасы, которые находятся непосредственно на складе и могут быть отгружены потребителям, и не учитывает, в частности, незавершенных поставок (так называемых «запасов в пути»). Между тем, при планировании поставок более удобным индикатором является суммарный уровень запасов (q), включающий - наряду со складскими запасами - также и уже заказанные объемы. Впрочем, все это актуально лишь в ситуациях, когда необходимость нового пополнения запасов может возникать еще до завершения предыдущей поставки.
Оптимизация процесса снабжения сводится к:
Прежде чем переходить к рассмотрению конкретных моделей управления запасами и условий их применимости, целесообразно обсудить ряд общих соображений, касающихся вида целевой функции (функции затрат).
Во-первых, речь будет идти о (средних) удельных затратах в единицу времени (по понятным причинам это удобнее, чем рассматривать суммарные затраты за весь период планирования).
Во-вторых, как отмечалось выше, искомые затраты распадаются на две части:
С = Сзк + Схр ,
где Сзк - затраты на закупку, Схр - затраты на хранение.
Следующее важнейшее соображение состоит в том, что при расчете каждой из величин Сзк и Схр затраты, не зависящие от организации процесса снабжения, можно не учитывать (они, конечно, войдут в суммарные затраты на закупку и хранение соответственно, но в целевую (подлежащую минимизации) функцию затрат их действительно можно не включать). Так, при расчете расходов на пополнение запасов нет смыла учитывать составляющие этих расходов, пропорциональные объемам поставок: ведь за достаточно длительный промежуток времени суммарный объем поставок оказывается приблизительно равным объему спроса, т.е. не зависит от организации процесса снабжения. В частности, это относится к стоимости закупаемых ресурсов, но при условии, что цена на них не зависит от объема поставок (при наличии скидок, зависящих от объема закупаемой партии, модель несколько усложняется, и этот случай должен рассматриваться отдельно).
Таким образом, в модели оптимизации управления запасами следует учитывать только те расходы на пополнение запасов, которые связаны с подготовкой, размещением, контролем исполнения и приемом заказа на закупку (и не зависят от объема поставки). Это, в частности, расходы на:
При учете транспортных затрат надлежит руководствоваться следующими соображениями. Если поставка связана с организацией специального рейса транспортного средства (самолета, автомобиля,, железнодорожного вагона, цистерны, контейнера) при его неполной загрузке, то стоимость этого рейса включается в постоянную (не зависящую от объема партии) составляющую издержек выполнения заказа, а из транспортных затрат исключается слагаемое, пропорциональное объему перевозки. При полной загрузке, напротив, остается только пропорциональное слагаемое, которое в издержки выполнения заказа не включается.
Стоимость хранения запасов (здесь также следует учитывать не все расходы) включает:
При расчете стоимости хранения расходы, не зависящие от величины запаса, в модели управления запасами не учитываются. Например, если все запасы размещаются на складе достаточно большой вместимости, причем избыточные мощности не используются, то стоимость складского помещения (включая плату за основные фонды, амортизационные отчисления, охрану, уборку помещения и т.д.) в стоимость хранения конкретной номенклатуры МТР не включается. В условиях же ограниченных складских помещений, когда решается вопрос об их распределении между различными продуктами или когда пустующие складские помещения могут быть использованы для других нужд (например, сданы в аренду сторонним организациям) стоимость складского помещения и техники переносится на стоимость хранения конкретного МТР пропорционально занимаемой им площади (емкости) склада. А именно, общая сумма соответствующих расходов (за единицу времени) делится на полезную площадь (емкость) склада и полученная величина умножается на площадь (соответственно объем), занимаемый единицей хранимого продукта.
Эксплуатационные расходы (на вспомогательные материалы, спецодежду, инвентаризацию, профилактические осмотры хранимого имущества и т.д.) могут либо определяться статистически по каждой номенклатуре в отдельности, либо также распределяться пропорционально площади (или емкости), занимаемой единицей хранения.
Некоторые статьи расходов на содержание запасов (в, частности, убытки от омертвления денежных средств, вложенных в запасы, которые обычно составляют значительную долю совокупных расходов на хранение) могут исчисляться пропорционально стоимости хранимого имущества. Распространен и такой подход, когда вся стоимость содержания запасов исчисляется как усредненная по множеству номенклатур процентная надбавка к стоимости. Однако такой подход, основанный на высокой доле затрат на иммобилизацию запасов (омертвление капитала), все-таки является сугубо приближенным и может не отражать реальных издержек хранения.
В соответствии с приведенными соображениями в экономико-математическую модель управления запасами целесообразно включить следующие два стоимостных параметра: издержки выполнения заказа (сзк) и удельные издержки хранения единицы рассматриваемого ресурса в единицу времени (схр).
Таблица 2
|
Параметр |
Обозначение |
|
Период планирования |
Тпл |
|
Цикл поставок (интервал между поставками) |
Т |
|
Объем партии заказа |
Q |
|
Минимальная партия поставки |
Qмин |
|
Максимальная партия поставки |
Qмакс |
|
Минимальная транзитная партия |
Qтр |
|
Время поставки - среднее значение - среднеквадратическое отклонение |
L σL |
|
Точка заказа |
s |
|
Максимальный уровень запаса |
S |
|
Интенсивность спроса (в единицу времени) - среднее значение - среднеквадратическое отклонение |
d σd |
|
Совокупный спрос за весь период планирования |
D |
|
Складской запас - текущий - страховой - совокупный |
qтек qстр qскл |
|
Суммарный объем запасов (включая запасы в пути) |
q |
|
Издержки выполнения заказа |
сзк |
|
Удельные издержки хранения |
схр |
|
Надежность обслуживания |
p |
Каждая из рассматриваемых ниже методик контроля запасов МТР направлена на минимизацию суммарных расходов на пополнение и хранение МТР при заданном уровне надежности обеспечения ими. Существенную часть этих расходов составляет стоимость оборотного капитала, вложенного в запасы, что в условиях нехватки оборотных средств делает задачу минимизации запасов особенно актуальной.
Эта модель предусматривает постоянный контроль уровня запасов. Заказ на пополнение запаса имеет фиксированный объем и формируется всякий раз, когда уровень запасов снижается до так называемой «точки заказа». Уровень «точки заказа» включает предполагаемый объем потребления рассматриваемого МТР за время реализации заказа и страховой запас, необходимый для обеспечения требуемого уровня надежности снабжения данным МТР при возможных колебаниях уровня спроса и времени реализации заказа.
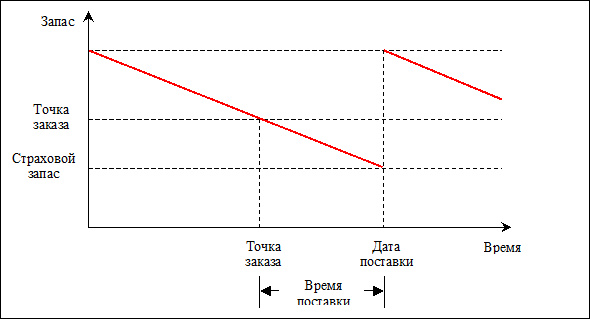
Величина партии заказа должна минимизировать суммарные рас


